Math 404 Topology

Ed Bueler:  474-7693
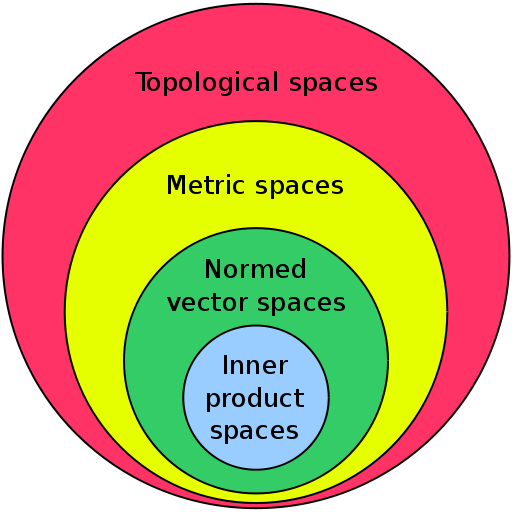
 elbueler@alaska.edu

Office: Chapman 301C (hours)

Class times and room:
 MWF 2:15 -- 3:15 pm
 Chapman 106

CRN:  75528

Syllabus

Required text:

  W. A. Sutherland, Introduction to
  Metric & Topological Spaces,
  2nd ed., Oxford U. Press 2009,
  ISBN-13: 978-0-19-956308-1
  (paperback; $28 new at amazon)


Links:

• When someone tries to explain or define "topology" they usually show Möbius strips, coffee mugs, Klein bottles, and stuff like that (Wikipedia). It is not wrong to show these more "algebraic" parts of topology, but it is misleading for students learning mathematics! Math 404 is a course in "point-set" or "general" topology.
• Two major definitions in the course are of metric spaces and topological spaces.
• Topological spaces generalize metric spaces, which in turn generalize the most useful kinds of vector spaces, namely topological vector spaces including Euclidean space.
  
• Topological spaces which are locally like Euclidean space are called manifolds, of which the Klein bottle is a (nonorientable) example.