This course covers numerical methods, and their analysis, for approximating partial differential equations (PDEs) and related problems on computers:  How to do it in practice.  How to determine how good a method is.  How to choose among algorithms when facing a hard problem.

There will be many computed examples.  Students will use Matlab/Octave to build algorithms and run them on concrete examples.  There is an emphasis on thinking with matrices and vectors.  We don't just list some finite difference schemes but try to think of them as matrix equations.  (We will write small codes to build big matrices for computer solution.)  I expose students to nonlinear examples because real problems are nonlinear.  Students are encouraged to come with a particular problems in mind, and to do a class project on it.

Topics include:  Heat equation: finite differences: explicit and implicit Fourier series stability convergence Transport equations (like waves): flux-conservation upwind finite differences and stability Lax, leapfrog, and Lax-Wendroff finite volume thinking The elliptic potential equation: boundary value problems finite differences eigenvalues of matrices sparse matrices Some real-world and nonlinear examples: nonlinear transport Newton's method Schroedinger equation

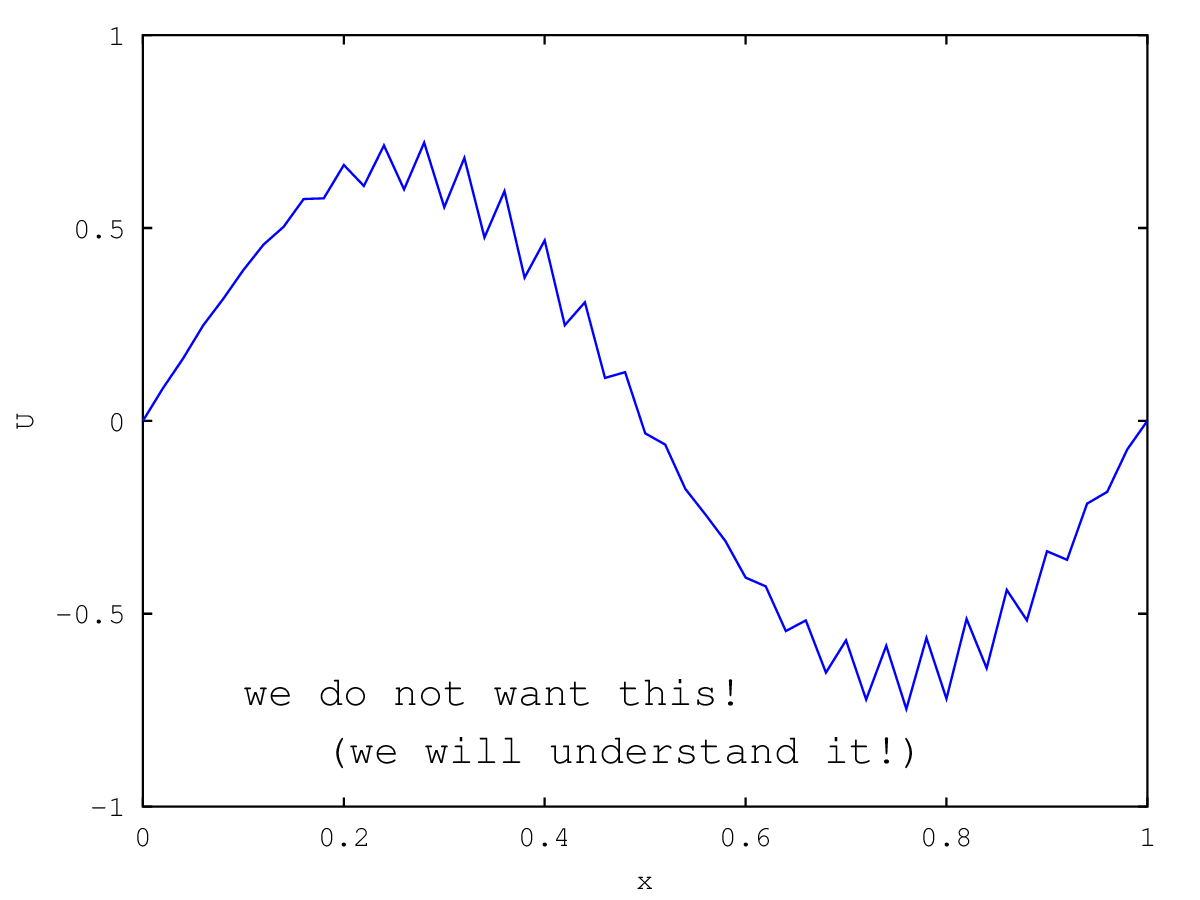
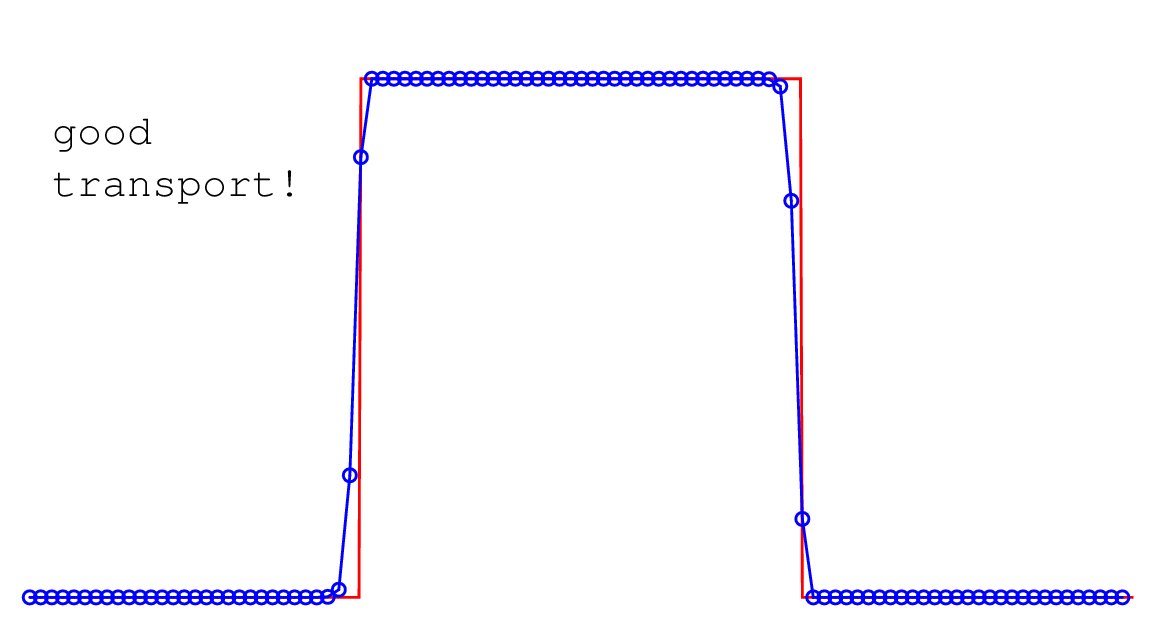
Prerequisites:  Officially, Prerequisites: CS F201, MATH F310, MATH F314, MATH F421, MATH F422 or permission of instructor.  Because you might be a graduate student with a background from another University (!), I would translate this as: Exposure to the use of computers to do mathematics (a numerical course of some kind like Math 310, ES 301, Phys 220, or at least CS 201) plus undergraduate differential equations (Math 302) plus undergraduate linear algebra (Math 314) plus some exposure to Fourier series and the method of separation of variables (Math 421 or Math/Phys 611).